AI Snake

Comparative Analysis of AI Methods for Snake Game: Heuristic, Q-learning, DQN, and PER

Introduction

The development of artificial intelligence (AI) has made significant strides, particularly in game playing. The Snake game, with its simple yet strategic gameplay, serves as an excellent platform for evaluating various AI approaches.
Reinforcement learning algorithms, such as Q-learning and Deep Q-Networks (DQN), have been successfully applied to master complex games like Go, Chess, and Atari games. The Snake game provides a challenging environment for AI agents to learn optimal policies through trial and error.
This report compares four AI methods for playing Snake: Heuristic, Q-learning, Deep Q-Networks (DQN), and Prioritized Experience Replay (PER), highlighting their implementations and performance.

GitHub Repository:

Overview

What is the Snake Game?

The Snake game is a classic arcade game where the player controls a snake that grows in length as it consumes food. The objective is to guide the snake to eat food while avoiding collisions with walls and its own body. The game ends when the snake collides with a wall or itself. The Snake game is challenging due to its dynamic environment and the need for strategic decision-making. The game’s simplicity makes it an ideal testbed for evaluating AI methods.

Stochastic Environments

The Snake game is a stochastic environment where the outcomes are not entirely predictable. The game involves randomness in the placement of food. The stochastic nature of the Snake game poses challenges for AI agents, requiring them to adapt to changing environments and make decisions under uncertainty.

Methodology for Implementation

Libraries and Tools

The implementation of the Snake game and AI methods requires the following libraries:

• pygame: for creating the game environment and handling user inputs.
• numpy: for numerical computations and array operations.
• pytorch: for implementing deep learning models and training neural networks.
• plotly: for visualizing the performance of AI methods.

Training Process

The training process involves the following steps:

1. Initialization: Initialize the game environment, AI agents, and performance metrics.
2. Game Loop: Interact with the game environment, select actions, and update the AI agents.
3. Training: Train the AI agents using reinforcement learning algorithms such as Q-learning, DQN, and PER.
4. Evaluation: Evaluate the performance of the AI agents based on metrics such as average score, variance, and standard deviation.
5. Visualization: Visualize the performance of the AI agents using graphs and plots.

For reinforcement learning algorithms, the training process involves iteratively updating the Q-values based on the rewards received and the observed states. The AI agents learn optimal policies through exploration and exploitation of the state-action space.

PER Agent after 5 episodes:

PER Agent after 200 episodes:

Evaluation Metrics

The performance of the AI methods is evaluated using different metrics that will be computed after 200 episodes of training. Those metrics will be computed during 200 episodes of training and will be used to compare the performance of the different AI methods. This makes a total of 200 episodes of training and evaluation for each AI method. This will allow us to compare the performance of the different AI methods when they have reached a stable performance level.

Evaluation Metrics

• Average Score: The average score achieved by the AI agent over the last 200 episodes.
• Variance of Score: The variance of the scores achieved by the AI agent over the last 200 episodes.
• Standard Deviation of Score: The standard deviation of the scores achieved by the AI agent over the last 200 episodes.
• Maximum Score: The maximum score achieved by the AI agent over the last 200 episodes.
• Minimum Score: The minimum score achieved by the AI agent over the last 200 episodes.
• Average Time per Episode: The average time taken by the AI agent to complete an episode over the last 200 episodes, in terms of the number of steps taken (or frames rendered).

Visualization

The performance of the AI methods will be visualized using graphs and plots to compare their evolution over time. The graphs will show the actual scores achieved by the AI agents over the training episodes, as well as other relevant metrics such as the evolution of the average score, last 10 games average score, and last 100 games average score. These visualizations will be created using the plotly library in Python.

By understanding these methods and their performance in a structured manner, we can better appreciate the strengths and weaknesses of each approach and identify the most effective strategy for mastering the Snake game. Let’s dive into the implementation of the AI methods and evaluate their performance.

Heuristic

Before diving into the AI methods, let’s first discuss the heuristic approach to playing Snake.

The heuristic method uses predefined rules to guide the snake’s movements. The heuristic approach is based on simple rules such as moving towards the food and avoiding collisions. The heuristic method is straightforward to implement but lacks adaptability to changing environments.

We are going to implement a simple heuristic method to play the Snake game and we will use it as a baseline to compare the performance of the AI methods.

Implementation

The ai_decision function is the heuristic method that determines the snake’s next move based on the relative positions of the snake’s head and the food.

Here is the ai_decision function

def ai_decision(snake_position, food_position, direction):
    """Heuristic Function to find the direction of the food while considering the current direction"""
    snake_x, snake_y = snake_position.x, snake_position.y
    food_x, food_y = food_position.x, food_position.y

    possible_moves = {
        'UP': (snake_x, snake_y - BLOCK_SIZE),
        'DOWN': (snake_x, snake_y + BLOCK_SIZE),
        'LEFT': (snake_x - BLOCK_SIZE, snake_y),
        'RIGHT': (snake_x + BLOCK_SIZE, snake_y)
    }

    if direction == Direction.UP:
        possible_moves.pop('DOWN')
    elif direction == Direction.DOWN:
        possible_moves.pop('UP')
    elif direction == Direction.LEFT:
        possible_moves.pop('RIGHT')
    elif direction == Direction.RIGHT:
        possible_moves.pop('LEFT')

    best_move = direction
    min_distance = float('inf')
    for move, (new_x, new_y) in possible_moves.items():
        distance = abs(new_x - food_x) + abs(new_y - food_y)
        if distance < min_distance:
            min_distance = distance
            best_move = move

    return best_move

The ai_decision function calculates the distance between the snake’s head and the food in each possible direction and selects the direction that minimizes the distance. The function considers the current direction of the snake to avoid moving in the opposite direction. The heuristic method is simple and effective for playing the Snake game.

Performance

The heuristic method achieves the following performance metrics after 200 games:

Metric	Value
Average Score	15.48
Variance	67.26
Standard Deviation	8.20
Maximum Score	41
Minimum Score	1
Average Moves	295.60

We will use these metrics as a baseline to compare the performance of the AI methods. Our goal is to develop AI agents that outperform the heuristic method in terms of those metrics. It would be nice to double the average score and the maximum score, while reducing the variance and standard deviation if possible.

AI Methods

Q-learning

Q-learning is a model-free reinforcement learning algorithm that seeks to find the optimal action-selection policy for any given finite Markov decision process (MDP). It does this by learning the value of state-action pairs, which are stored in a table known as the Q-table.

More about Q-learning theorie

Q-learning updates the Q-values based on the agent’s experiences, gradually converging towards the optimal policy. The agent explores the state-action space, selects actions based on an exploration-exploitation strategy, and receives rewards that influence future decisions. This iterative process enables the agent to learn from both positive and negative outcomes.

Q-learning is based on the Bellman equation, which provides a recursive decomposition of the value function. The Q-value of a state-action pair $(s, a)$ represents the expected utility of taking action $a$ in state $s$ and following the optimal policy thereafter.

The Q-learning update rule is given by:

\[Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ r_{t+1} + \gamma \max_{a} Q(s_{t+1}, a) - Q(s_t, a_t) \right]\]

where:

• $Q(s_t, a_t)$ is the current Q-value of state $s_t$ and action $a_t$,
• $\alpha$ is the learning rate (step size),
• $r_{t+1}$ is the reward received after taking action $a_t$ in state $s_t$,
• $\gamma$ is the discount factor, which represents the importance of future rewards,
• $s_{t+1}$ is the next state,
• $\max_{a} Q(s_{t+1}, a)$ is the maximum Q-value for the next state $s_{t+1}$ across all possible actions.

The Q-learning algorithm follows these steps:

1. Initialize the Q-table with arbitrary values.
2. For each episode:
   • Initialize the starting state $s_0$.
   • For each step in the episode:
     • Choose an action $a_t$ based on the current state $s_t$ using an exploration-exploitation strategy (e.g., $\epsilon$-greedy).
     • Execute the action $a_t$ and observe the reward $r_{t+1}$ and next state $s_{t+1}$.
     • Update the Q-value $Q(s_t, a_t)$ using the Q-learning update rule.
     • Set $s_{t+1}$ as the current state $s_t$.
3. Repeat until the Q-values converge or a stopping criterion is met.

Q-learning’s ability to learn the optimal policy without requiring a model of the environment makes it a powerful and versatile algorithm in reinforcement learning¹.

Q-learning in Snake Game

In the context of the Snake game, Q-learning is applied to train the snake to navigate the environment, consume food, and avoid collisions with walls and itself. The Snake game is modeled as a Markov decision process (MDP), where:

• States: The state of the game is defined by the position of the snake’s head, the positions of the food, and the direction of the snake’s movement. Additionally, the state may include information about the snake’s body segments and potential collisions.
• Actions: The possible actions the snake can take are moving left, right, up, or down.
• Rewards: The reward function is designed to encourage the snake to eat food and survive. A positive reward is given when the snake eats the food, while a negative reward is given when the snake collides with a wall or its own body.

To implement Q-learning for the Snake game, the following steps are taken:

1. State Representation: The state is represented as a tuple or list that includes the coordinates of the snake’s head, the relative position of the food, and the direction of movement. This compact representation captures the essential information needed for decision-making.

2. Initialization: The Q-table is initialized with arbitrary values. The Q-table maps each state-action pair to a Q-value, representing the expected utility of taking a particular action in a given state.

3. Exploration-Exploitation Strategy: An exploration-exploitation strategy, such as $\epsilon$-greedy, is used to balance exploration of new actions and exploitation of known rewarding actions. With probability $\epsilon$, a random action is selected (exploration), and with probability $1 - \epsilon$, the action with the highest Q-value is chosen (exploitation).

4. Q-value Update: During each episode, the agent updates the Q-values based on the rewards received. The update rule is applied to adjust the Q-values towards the observed rewards and future expected rewards.

5. Learning and Decay: The learning rate $\alpha$ determines the extent to which new information overrides old information. Over time, $\epsilon$ is decayed to reduce exploration and increase exploitation, allowing the agent to focus on the learned optimal policy.

Implementation

The Q-learning agent is implemented using a Python class that encapsulates the Q-learning algorithm for the Snake game. The agent interacts with the game environment, selects actions based on the Q-values, and updates the Q-values based on the rewards received.

Here is the Q-learning implementation

The QLearningAgent class implements the Q-learning algorithm for the Snake game. The class includes methods for getting the state representation, selecting actions based on the Q-values, updating the Q-values, and decaying the exploration rate $\epsilon$. The get_state method extracts relevant information from the game environment to represent the state. The act method selects actions based on the Q-values and the exploration rate. The update_q_value method updates the Q-values based on the rewards and next state. The decay_epsilon method reduces the exploration rate over time to focus on exploitation.

agent.py

import numpy as np
import random
from collections import deque
from snake_game import Direction, Point, SnakeGameAI

class QLearningAgent:
    def __init__(self, actions):
        self.actions = actions
        self.step_size = 0.3
        self.gamma = 0.9
        self.epsilon = 1.0
        self.epsilon_decay_rate = 0.95
        self.min_epsilon = 0.001
        self.q_table = dict()

    def get_state(self, game):
        head = game.snake[0]
        point_l = Point(head.x - 20, head.y)
        point_r = Point(head.x + 20, head.y)
        point_u = Point(head.x, head.y - 20)
        point_d = Point(head.x, head.y + 20)

        dir_l = game.direction == Direction.LEFT
        dir_r = game.direction == Direction.RIGHT
        dir_u = game.direction == Direction.UP
        dir_d = game.direction == Direction.DOWN

        state = [
            dir_l,
            dir_r,
            dir_u,
            dir_d,
            game.food.x < game.head.x,
            game.food.x > game.head.x,
            game.food.y < game.head.y,
            game.food.y > game.head.y,
            game.is_collision(point_l),
            game.is_collision(point_r),
            game.is_collision(point_u),
            game.is_collision(point_d)
        ]

        return tuple(state)

    def act(self, state):
        if state not in self.q_table:
            self.q_table[state] = {a: 0.0 for a in self.actions}

        if np.random.rand() <= self.epsilon:
            return random.choice(self.actions)

        q_values = self.q_table[state]
        max_q = max(q_values.values())
        actions_with_max_q = [a for a, q in q_values.items() if q == max_q]

        return random.choice(actions_with_max_q)

    def update_q_value(self, state, reward, action, next_state, done):
        if next_state not in self.q_table:
            self.q_table[next_state] = {a: 0.0 for a in self.actions}

        max_q_next = max(self.q_table[next_state].values())
        self.q_table[state][action] += self.step_size * (
            reward + self.gamma * max_q_next * (1.0 - done) - self.q_table[state][action]
        )

    def decay_epsilon(self):
        self.epsilon = max(self.min_epsilon, self.epsilon * self.epsilon_decay_rate)

The training loop interacts with the Snake game environment, updates the Q-values, and decays the exploration rate over time. The agent learns optimal policies by exploring the state-action space and updating the Q-values based on the rewards received.

train.py

from agent import QLearningAgent
from snake_game import SnakeGameAI
from utils import plot, compute_statistics, print_statistics

def train():
    actions = [0, 1, 2]  
    agent = QLearningAgent(actions)
    game = SnakeGameAI()

    scores = []
    moves_list = []  # Liste pour enregistrer les mouvements
    mean_scores = []
    last_10_mean_scores = []
    last_100_mean_scores = []
    total_score = 0

    for game_number in range(1, 1001):
        game.reset()  
        state = agent.get_state(game)
        score = 0
        moves = 0

        while True:
            action = agent.act(state)
            final_move = [0, 0, 0]
            final_move[action] = 1

            reward, done, score = game.play_step(final_move)
            next_state = agent.get_state(game)

            agent.update_q_value(state, reward, action, next_state, done)

            state = next_state
            moves += 1

            if done:
                agent.decay_epsilon()
                scores.append(score)
                moves_list.append(moves)  # Enregistrer les mouvements de cette partie
                total_score += score
                mean_score = total_score / game_number
                mean_scores.append(mean_score)

                if len(scores) >= 10:
                    last_10_mean_score = sum(scores[-10:]) / 10
                else:
                    last_10_mean_score = sum(scores) / len(scores)
                last_10_mean_scores.append(last_10_mean_score)

                if len(scores) >= 100:
                    last_100_mean_score = sum(scores[-100:]) / 100
                else:
                    last_100_mean_score = sum(scores) / len(scores)
                last_100_mean_scores.append(last_100_mean_score)

                print(f'Game {game_number}, Score: {score}, Moves: {moves}, Average Score: {mean_score:.2f}')

                break

    plot(scores, mean_scores, last_10_mean_scores, last_100_mean_scores)

    last_200_scores = scores[-200:]
    last_200_moves = moves_list[-200:]  # Utiliser les mouvements enregistrés
    statistics = compute_statistics(last_200_scores, last_200_moves)

    print_statistics(statistics)

if __name__ == "__main__":
    train()

Performance

Here are the performance metrics for the Q-learning:

Metric	Value
Average Score	30.64
Variance	170.99
Standard Deviation	13.08
Maximum Score	66
Minimum Score	1
Average Moves	788.80

If we compare the performance of the Q-learning agent with the heuristic method, we observe an improvement in the average score and maximum score. The Q-learning agent has learned a policy that achieves higher scores on average and can handle more complex scenarios in the Snake game. The maximum score of 66 indicates that the Q-learning agent can achieve a high score by learning optimal policies. However, there is still room for improvement in reducing the variance and standard deviation of the scores.

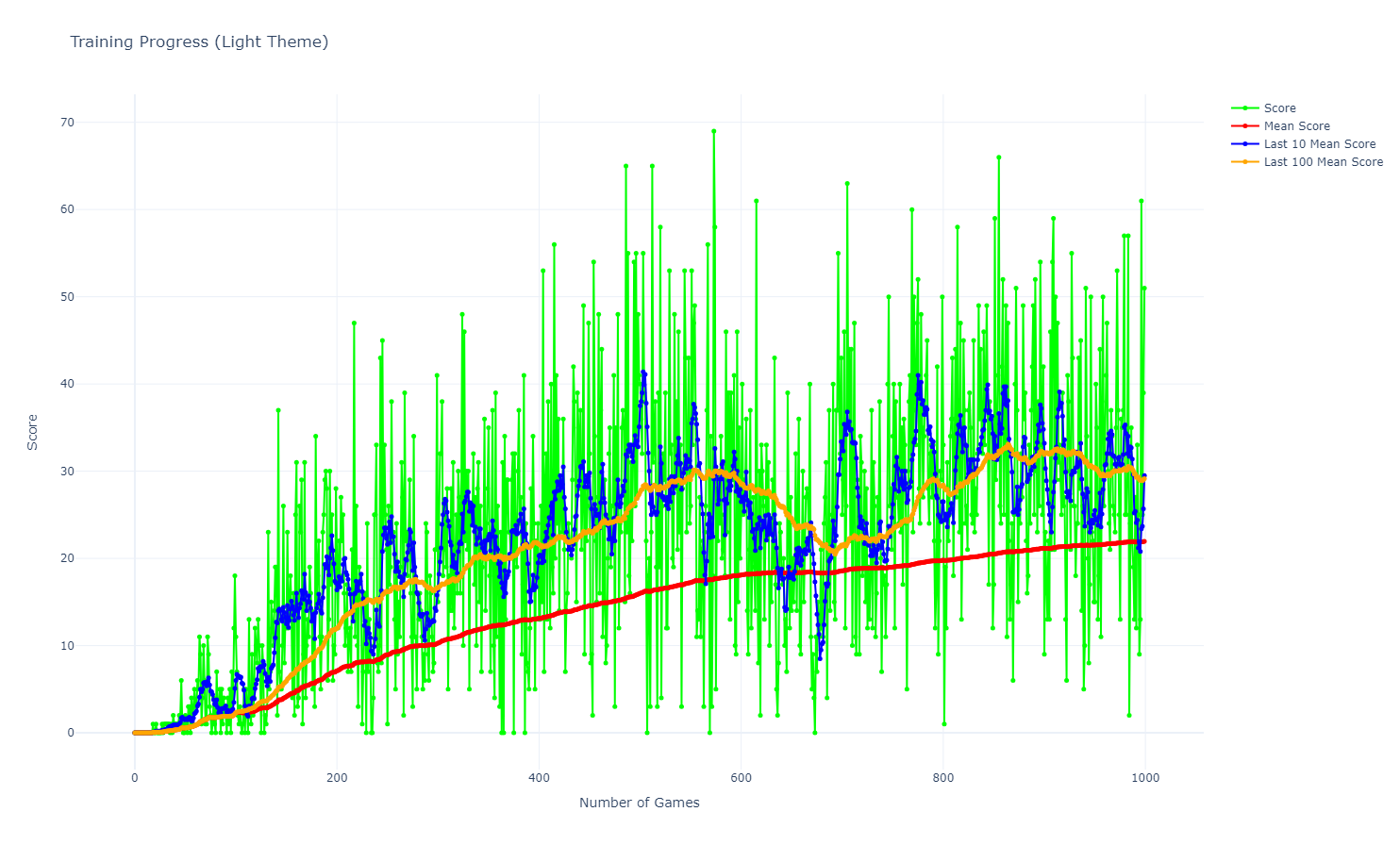
Visualisation

The graph shows the evolution of the average score, last 10 games average score, and last 100 games average score over the training episodes. The Q-learning agent’s performance improves over time, indicating learning progress and convergence towards optimal policies.

We can see that the convergence is not perfect, as there are fluctuations in the scores, leading to variance in the performance metrics. However, it looks like the convergence happens around the 500th episode, but it’s not stable yet.

To improve the performance and stability of the Q-learning agent, we can explore advanced techniques such as Deep Q-Networks (DQN) and Prioritized Experience Replay (PER). These methods leverage deep learning and experience replay to enhance learning efficiency and robustness in reinforcement learning tasks. We will start by implementing DQN and then extend it with PER to evaluate their impact on the Snake game performance.

Deep Q-Networks (DQN)

Deep Q-Networks (DQN) combine deep learning with Q-learning to approximate the action-value function. DQN uses a neural network to approximate the Q-values and update the network weights through backpropagation. This approach is effective for learning optimal policies in high-dimensional state-action spaces.

Neural Network

What is a Neural Network?

A neural network is a computational model inspired by the structure and function of the human brain. It consists of interconnected nodes (neurons) organized in layers. Neural networks are used to learn complex patterns and relationships in data, making them suitable for tasks such as image recognition, natural language processing, and game playing.

How Does a Neural Network Work?

1. Input Layer: Receives the input data.
2. Hidden Layers: Process the input through weighted connections and activation functions.
3. Output Layer: Produces the network’s predictions or classifications.

Neural networks learn by adjusting the weights of the connections between neurons to minimize the difference between predicted and actual outputs. This process, known as backpropagation, involves propagating errors backward through the network to update the weights.

More details about DQN here

DQN builds on the foundation of Q-learning by leveraging a neural network to represent the Q-function, which maps state-action pairs to their respective Q-values. The primary components of DQN include:

1. Experience Replay: This technique involves storing the agent’s experiences at each time step in a replay buffer. During training, random samples from this buffer are used to update the Q-network. This helps to break the correlations between consecutive experiences and improves the stability of the training process.

2. Fixed Q-Targets: To mitigate the instability caused by the rapidly changing target values, DQN uses a separate target network to generate the target Q-values. This target network is updated periodically with the weights of the primary Q-network, providing more stable target values.

The DQN Loss Function

The Q-network is trained to minimize the loss function defined as:

\[L(\theta) = \mathbb{E}_{(s, a, r, s') \sim \mathcal{D}} \left[ \left( r + \gamma \max_{a'} Q(s', a'; \theta^-) - Q(s, a; \theta) \right)^2 \right]\]

where:

• $ \theta $ are the parameters of the Q-network.
• $ \theta^- $ are the parameters of the target network.
• $ s $ and $ s’ $ are the current and next states, respectively.
• $ a $ is the action taken.
• $ r $ is the reward received.
• $ \gamma $ is the discount factor.
• $ \mathcal{D} $ is the replay buffer.

The neural network architecture typically consists of an input layer, one or more hidden layers, and an output layer that predicts Q-values for each possible action.²

Implementation

The DQN agent is implemented using a neural network to approximate the Q-values and a replay buffer to store experiences. The agent interacts with the game environment, updates the Q-network, and samples experiences for training.

Here is the DQN implemetation

Neural Network Architecture: - The input layer receives the state representation. - Hidden layers process the input using activation functions (e.g., ReLU). - The output layer produces Q-values for each action.

model.py

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

class DQN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(DQN, self).__init__()
        self.linear1 = nn.Linear(input_size, hidden_size)
        self.linear2 = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        x = F.relu(self.linear1(x))
        x = self.linear2(x)
        return x

class QTrainer:
    def __init__(self, model, lr, gamma):
        self.model = model
        self.lr = lr
        self.gamma = gamma
        self.optimizer = optim.Adam(model.parameters(), lr=self.lr)
        self.criterion = nn.MSELoss()

    def train_step(self, state, action, reward, next_state, done):
        state = torch.tensor(state, dtype=torch.float)
        next_state = torch.tensor(next_state, dtype=torch.float)
        action = torch.tensor(action, dtype=torch.long)
        reward = torch.tensor(reward, dtype=torch.float)

        if len(state.shape) == 1:
            state = torch.unsqueeze(state, 0)
            next_state = torch.unsqueeze(next_state, 0)
            action = torch.unsqueeze(action, 0)
            reward = torch.unsqueeze(reward, 0)
            done = (done, )

        pred = self.model(state)
        target = pred.clone()
        for idx in range(len(done)):
            Q_new = reward[idx]
            if not done[idx]:
                Q_new = reward[idx] + self.gamma * torch.max(self.model(next_state[idx]))
            target[idx][torch.argmax(action[idx]).item()] = Q_new

        self.optimizer.zero_grad()
        loss = self.criterion(target, pred)
        loss.backward()
        self.optimizer.step()

Agent Class: - Initializes the Q-network and replay buffer. - Handles action selection using an epsilon-greedy strategy. - Updates the Q-network using experiences from the replay buffer.

agent.py

import torch
import random
import numpy as np
from collections import deque
from model import DQN, QTrainer
from snake_game import Direction, Point, SnakeGameAI

MAX_MEMORY = 100_000
BATCH_SIZE = 512
LR = 0.001

class Agent:
    def __init__(self):
        self.n_games = 0
        self.epsilon = 0  
        self.gamma = 0.9 
        self.memory = deque(maxlen=MAX_MEMORY)
        self.model = DQN(11, 256, 3)
        self.trainer = QTrainer(self.model, lr=LR, gamma=self.gamma)

    def get_state(self, game):
        head = game.snake[0]
        point_l = Point(head.x - 20, head.y)
        point_r = Point(head.x + 20, head.y)
        point_u = Point(head.x, head.y - 20)
        point_d = Point(head.x, head.y + 20)

        dir_l = game.direction == Direction.LEFT
        dir_r = game.direction == Direction.RIGHT
        dir_u = game.direction == Direction.UP
        dir_d = game.direction == Direction.DOWN

        state = [
            (dir_r and game.is_collision(point_r)) or 
            (dir_l and game.is_collision(point_l)) or 
            (dir_u and game.is_collision(point_u)) or 
            (dir_d and game.is_collision(point_d)),

            (dir_u and game.is_collision(point_r)) or 
            (dir_d and game.is_collision(point_l)) or 
            (dir_l and game.is_collision(point_u)) or 
            (dir_r and game.is_collision(point_d)),

            (dir_d and game.is_collision(point_r)) or 
            (dir_u and game.is_collision(point_l)) or 
            (dir_r and game.is_collision(point_u)) or 
            (dir_l and game.is_collision(point_d)),

            dir_l,
            dir_r,
            dir_u,
            dir_d,

            game.food.x < game.head.x,
            game.food.x > game.head.x,
            game.food.y < game.head.y,
            game.food.y > game.head.y
        ]

        return np.array(state, dtype=int)

    def remember(self, state, action, reward, next_state, done):
        self.memory.append((state, action, reward, next_state, done))

    def train_long_memory(self):
        if len(self.memory) > BATCH_SIZE:
            mini_sample = random.sample(self.memory, BATCH_SIZE)
        else:
            mini_sample = self.memory

        states, actions, rewards, next_states, dones = zip(*mini_sample)
        self.trainer.train_step(states, actions, rewards, next_states, dones)

    def train_short_memory(self, state, action, reward, next_state, done):
        self.trainer.train_step(state, action, reward, next_state, done)

    def get_action(self, state):
        self.epsilon = 80 - self.n_games
        final_move = [0, 0, 0]
        if random.randint(0, 200) < self.epsilon:
            move = random.randint(0, 2)
            final_move[move] = 1
        else:
            state0 = torch.tensor(state, dtype=torch.float)
            prediction = self.model(state0)
            move = torch.argmax(prediction).item()
            final_move[move] = 1
        return final_move

Training Loop: - Initializes the game environment and agent. - Executes the training loop, interacting with the environment and updating the Q-network. - Tracks performance metrics and visualizes the results.

train.py

from agent import Agent
from snake_game import SnakeGameAI

from utils import plot, compute_statistics, print_statistics


def train():
    scores = []
    moves = []
    mean_scores = []
    last_10_mean_scores = []
    last_100_mean_scores = []
    total_score = 0
    record = 0
    agent = Agent()
    game = SnakeGameAI()
    
    while agent.n_games < 400:
        state_old = agent.get_state(game)
        final_move = agent.get_action(state_old)
        reward, done, score = game.play_step(final_move)
        state_new = agent.get_state(game)

        agent.train_short_memory(state_old, final_move, reward, state_new, done)
        agent.remember(state_old, final_move, reward, state_new, done)

        moves.append(game.frame_iteration)

        if done:
            game.reset()
            agent.n_games += 1
            agent.train_long_memory()

            if score > record:
                record = score

            print(f'Game {agent.n_games}, Score: {score}, Record: {record}')

            scores.append(score)
            total_score += score
            mean_score = total_score / agent.n_games
            mean_scores.append(mean_score)
            if len(scores) >= 10:
                last_10_mean_score = sum(scores[-10:]) / 10
            else:
                last_10_mean_score = sum(scores) / len(scores)
            last_10_mean_scores.append(last_10_mean_score)

            if len(scores) >= 100:
                last_100_mean_score = sum(scores[-100:]) / 100
            else:
                last_100_mean_score = sum(scores) / len(scores)
            last_100_mean_scores.append(last_100_mean_score)

            if agent.n_games % 200 == 0:
                plot(scores, mean_scores, last_10_mean_scores, last_100_mean_scores)

    last_200_scores = scores[-200:]
    last_200_moves = moves[-200:]
    statistics = compute_statistics(last_200_scores, last_200_moves)

    print_statistics(statistics)

if __name__ == '__main__':
    train()

Performance

Statistics for the last 200 games:

Metric	Value
Average Score	29.16
Variance	152.71
Standard Deviation	12.36
Maximum Score	65
Minimum Score	1
Average Moves	1056.50

If we compare the performance of the DQN agent with the Q-learning agent, we observe that the DQN agent achieves a comparable average score and maximum score. However, we were able to reduce the variance and standard deviation of the scores, indicating improved stability and consistency in performance. The DQN agent’s average moves per game are higher, suggesting more complex decision-making and exploration of the state-action space. The minimum score of 1 means that the agent still encounters challenges in certain scenarios. The DQN agent’s performance is promising, but there is room for further optimization and learning.

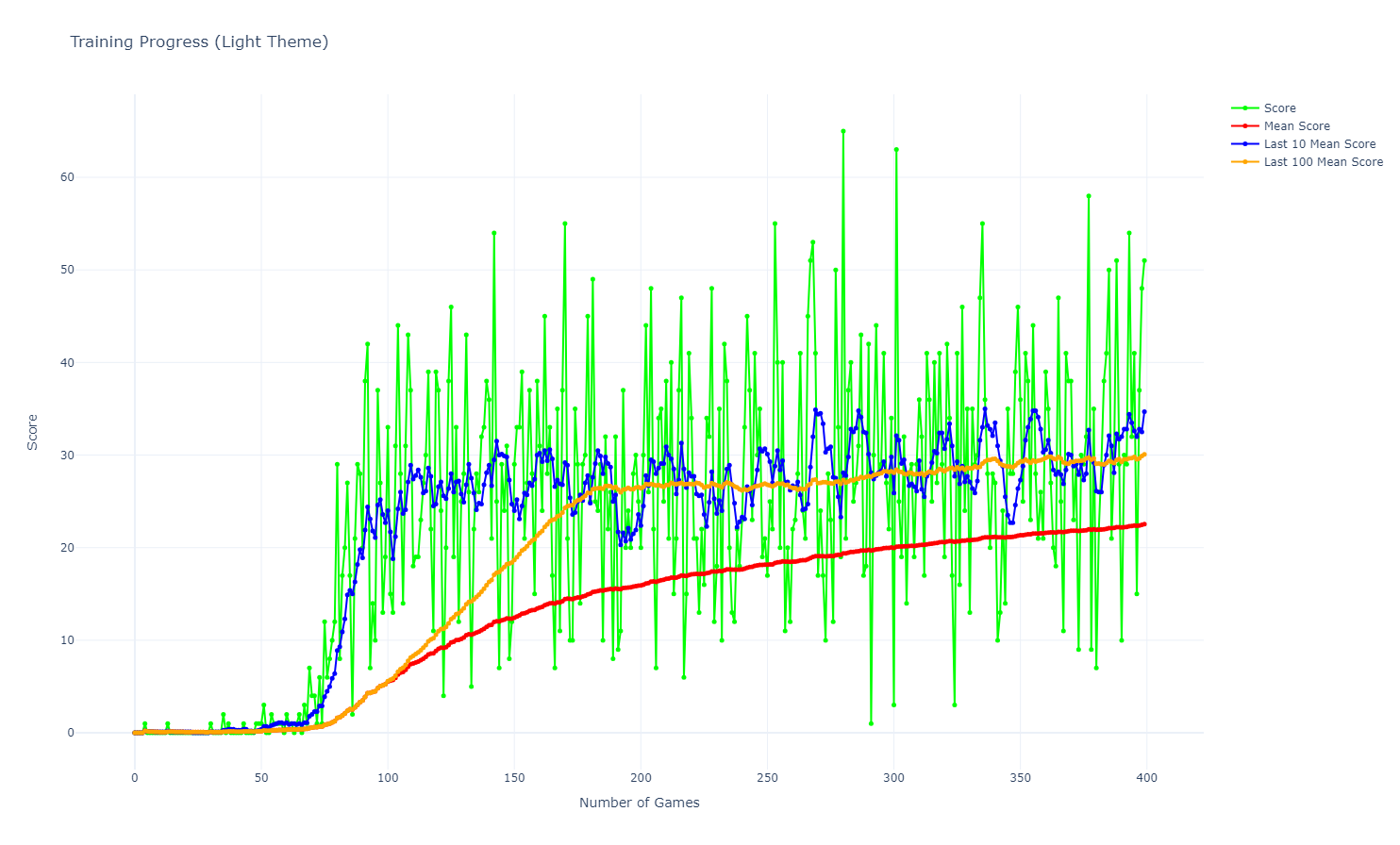
Visualisation

The graph shows the evolution of the average score, last 10 games average score, and last 100 games average score over the training episodes. The DQN agent’s performance improves over time, indicating learning progress and convergence towards optimal policies. The convergence is more stable compared to Q-learning, with reduced fluctuations in the scores.

To improve the learning efficiency and performance further, we can introduce Prioritized Experience Replay (PER), which prioritizes experiences based on their importance in learning. PER enhances the exploration and exploitation trade-off by focusing on experiences that contribute the most to learning.

Prioritized Experience Replay (PER)

Prioritized Experience Replay (PER) is an enhancement of the standard DQN algorithm that improves the efficiency of learning by prioritizing experiences based on their temporal-difference error. This approach helps the agent to focus on more significant experiences, leading to faster and more stable convergence.

More details about PER here

In standard Experience Replay, each experience in the replay buffer has an equal probability of being selected for training. However, not all experiences are equally important for learning. Some experiences, such as those with large temporal-difference (TD) errors, provide more informative updates to the Q-network. PER addresses this by assigning a priority to each experience based on its TD error, allowing the agent to sample more important experiences more frequently.

Priority

The priority $ p_i $ of an experience $ i $ is typically defined as:

\[p_i = \left( |\delta_i| + \epsilon \right)^\alpha\]

where:

• $ \delta_i $ is the TD error of experience $ i $.
• $ \epsilon $ is a small positive constant to ensure that all experiences have a non-zero probability of being selected.
• $ \alpha $ determines the level of prioritization, with $ \alpha = 0 $ corresponding to uniform sampling.

Sampling

To ensure the replay buffer remains stable, PER also includes importance-sampling weights to correct for the bias introduced by prioritized sampling. The importance-sampling weight $ w_i $ for experience $ i $ is given by:

\[w_i = \left( \frac{1}{N} \cdot \frac{1}{P(i)} \right)^\beta\]

where:

• $ N $ is the total number of experiences in the replay buffer.
• $ P(i) $ is the probability of sampling experience $ i $.
• $ \beta $ controls the amount of importance-sampling correction, with $ \beta = 1 $ providing full correction.

Prioritized Experience Replay enhances the learning process by focusing on experiences that contribute the most to the agent’s learning progress. By prioritizing informative experiences, the agent can learn more efficiently and achieve better performance in reinforcement learning tasks.³

Implementation

The PER implementation extends the DQN agent by incorporating a prioritized replay buffer and importance-sampling weights. The agent prioritizes experiences based on their TD errors and samples experiences with probabilities proportional to their priorities.

Here is the PER implementation

The PER implementation for the Snake game extends the standard DQN algorithm by incorporating the prioritized replay buffer. The key components of the PER implementation are:

Neural Network Architecture:

• The Q-network architecture remains the same as in the DQN implementation.

model.py

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

class LinearQNet(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(LinearQNet, self).__init__()
        self.linear1 = nn.Linear(input_size, hidden_size)
        self.linear2 = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        x = F.relu(self.linear1(x))
        x = self.linear2(x)
        return x

class QTrainer:
    def __init__(self, model, lr, gamma):
        self.model = model
        self.lr = lr
        self.gamma = gamma
        self.optimizer = optim.Adam(model.parameters(), lr=self.lr)
        self.criterion = nn.MSELoss()

    def train_step(self, state, action, reward, next_state, done, weights):
        state = torch.tensor(state, dtype=torch.float)
        next_state = torch.tensor(next_state, dtype=torch.float)
        action = torch.tensor(action, dtype=torch.long)
        reward = torch.tensor(reward, dtype=torch.float)
        weights = torch.tensor(weights, dtype=torch.float)

        if len(state.shape) == 1:
            state = torch.unsqueeze(state, 0)
            next_state = torch.unsqueeze(next_state, 0)
            action = torch.unsqueeze(action, 0)
            reward = torch.unsqueeze(reward, 0)
            done = (done, )
            weights = torch.unsqueeze(weights, 0)

        pred = self.model(state)
        target = pred.clone()
        for idx in range(len(done)):
            Q_new = reward[idx]
            if not done[idx]:
                Q_new = reward[idx] + self.gamma * torch.max(self.model(next_state[idx]))
            target[idx][action[idx].argmax().item()] = Q_new

        self.optimizer.zero_grad()
        loss = (self.criterion(target, pred) * weights).mean()
        loss.backward()
        self.optimizer.step()

Prioritized Replay Buffer & Agent Class are implemented as follows:

Prioritized Replay Buffer:

• Stores experiences with priorities based on their TD errors.
• Uses a sum tree data structure to efficiently sample experiences based on their priorities.
• Samples experiences based on their priorities.

Agent Class:

• Initializes the prioritized replay buffer.
• Updates the priorities of experiences in the buffer based on their TD errors.
• Corrects for sampling bias using importance-sampling weights.

agent.py

import torch
import random
import numpy as np
from collections import deque
from model import LinearQNet, QTrainer
from snake_game import Direction, Point, SnakeGameAI
import heapq

MAX_MEMORY = 100_000
BATCH_SIZE = 512
LR = 0.001
ALPHA = 0.6
BETA = 0.4

class SumTree:
    def __init__(self, capacity):
        self.capacity = capacity
        self.tree = np.zeros(2 * capacity - 1)
        self.data = np.zeros(capacity, dtype=object)
        self.write = 0

    def _propagate(self, idx, change):
        parent = (idx - 1) // 2
        self.tree[parent] += change
        if parent != 0:
            self._propagate(parent, change)

    def update(self, idx, p):
        change = p - self.tree[idx]
        self.tree[idx] = p
        self._propagate(idx, change)

    def add(self, p, data):
        idx = self.write + self.capacity - 1
        self.data[self.write] = data
        self.update(idx, p)
        self.write += 1
        if self.write >= self.capacity:
            self.write = 0

    def _retrieve(self, idx, s):
        left = 2 * idx + 1
        right = left + 1
        if left >= len(self.tree):
            return idx
        if s <= self.tree[left]:
            return self._retrieve(left, s)
        else:
            return self._retrieve(right, s - self.tree[left])

    def get(self, s):
        idx = self._retrieve(0, s)
        dataIdx = idx - self.capacity + 1
        return idx, self.tree[idx], self.data[dataIdx]

    def total(self):
        return self.tree[0]

class PrioritizedReplayBuffer:
    def __init__(self, capacity):
        self.tree = SumTree(capacity)

    def add(self, error, sample):
        p = (error + 1e-5) ** ALPHA
        self.tree.add(p, sample)

    def sample(self, n):
        batch = []
        idxs = []
        segment = self.tree.total() / n
        priorities = []
        for i in range(n):
            a = segment * i
            b = segment * (i + 1)
            s = random.uniform(a, b)
            idx, p, data = self.tree.get(s)
            priorities.append(p)
            batch.append(data)
            idxs.append(idx)
        sampling_probabilities = priorities / self.tree.total()
        is_weight = np.power(self.tree.capacity * sampling_probabilities, -BETA)
        is_weight /= is_weight.max()
        return idxs, batch, is_weight

    def update(self, idx, error):
        p = (error + 1e-5) ** ALPHA
        self.tree.update(idx, p)

class Agent:
    def __init__(self):
        self.n_games = 0
        self.epsilon = 0
        self.gamma = 0.9
        self.memory = PrioritizedReplayBuffer(MAX_MEMORY)
        self.model = LinearQNet(11, 256, 3)
        self.trainer = QTrainer(self.model, lr=LR, gamma=self.gamma)

    def get_state(self, game):
        head = game.snake[0]
        point_l = Point(head.x - 20, head.y)
        point_r = Point(head.x + 20, head.y)
        point_u = Point(head.x, head.y - 20)
        point_d = Point(head.x, head.y + 20)

        dir_l = game.direction == Direction.LEFT
        dir_r = game.direction == Direction.RIGHT
        dir_u = game.direction == Direction.UP
        dir_d = game.direction == Direction.DOWN

        state = [
            (dir_r and game.is_collision(point_r)) or 
            (dir_l and game.is_collision(point_l)) or 
            (dir_u and game.is_collision(point_u)) or 
            (dir_d and game.is_collision(point_d)),

            (dir_u and game.is_collision(point_r)) or 
            (dir_d and game.is_collision(point_l)) or 
            (dir_l and game.is_collision(point_u)) or 
            (dir_r and game.is_collision(point_d)),

            (dir_d and game.is_collision(point_r)) or 
            (dir_u and game.is_collision(point_l)) or 
            (dir_r and game.is_collision(point_u)) or 
            (dir_l and game.is_collision(point_d)),

            dir_l,
            dir_r,
            dir_u,
            dir_d,

            game.food.x < game.head.x,
            game.food.x > game.head.x,
            game.food.y < game.head.y,
            game.food.y > game.head.y
        ]

        return np.array(state, dtype=int)

    def remember(self, state, action, reward, next_state, done):
        target = self.trainer.model(torch.tensor(state, dtype=torch.float))
        with torch.no_grad():
            target_val = self.trainer.model(torch.tensor(next_state, dtype=torch.float))
        target = target[action]
        target_val = reward + (1 - done) * self.gamma * torch.max(target_val)
        error = abs(target - target_val).argmax().item()
        self.memory.add(error, (state, action, reward, next_state, done))

    def train_long_memory(self):
        if self.memory.tree.total() > BATCH_SIZE:
            idxs, mini_batch, is_weight = self.memory.sample(BATCH_SIZE)
        else:
            idxs, mini_batch, is_weight = self.memory.sample(int(self.memory.tree.total()))
        
        states, actions, rewards, next_states, dones = zip(*mini_batch)
        self.trainer.train_step(states, actions, rewards, next_states, dones, is_weight)

    def train_short_memory(self, state, action, reward, next_state, done):
        self.trainer.train_step(state, action, reward, next_state, done, np.ones(1))

    def get_action(self, state):
        self.epsilon = 80 - self.n_games
        final_move = [0, 0, 0]
        if random.randint(0, 200) < self.epsilon:
            move = random.randint(0, 2)
            final_move[move] = 1
        else:
            state0 = torch.tensor(state, dtype=torch.float)
            prediction = self.model(state0)
            move = torch.argmax(prediction).item()
            final_move[move] = 1
        return final_move

Training Loop:

• Initializes the game environment and agent.
• Executes the training loop, interacting with the environment and updating the PER agent.
• Tracks performance metrics and visualizes the results.

train.py

from agent import Agent
from snake_game import SnakeGameAI

from utils import plot, compute_statistics, print_statistics


def train():
    scores = []
    moves = []
    mean_scores = []
    last_10_mean_scores = []
    last_100_mean_scores = []
    total_score = 0
    record = 0
    agent = Agent()
    game = SnakeGameAI()
    
    while agent.n_games < 400:
        state_old = agent.get_state(game)
        final_move = agent.get_action(state_old)
        reward, done, score = game.play_step(final_move)
        state_new = agent.get_state(game)

        agent.train_short_memory(state_old, final_move, reward, state_new, done)
        agent.remember(state_old, final_move, reward, state_new, done)

        moves.append(game.frame_iteration)

        if done:
            game.reset()
            agent.n_games += 1
            agent.train_long_memory()

            if score > record:
                record = score

            print(f'Game {agent.n_games}, Score: {score}, Record: {record}')

            scores.append(score)
            total_score += score
            mean_score = total_score / agent.n_games
            mean_scores.append(mean_score)
            if len(scores) >= 10:
                last_10_mean_score = sum(scores[-10:]) / 10
            else:
                last_10_mean_score = sum(scores) / len(scores)
            last_10_mean_scores.append(last_10_mean_score)

            if len(scores) >= 100:
                last_100_mean_score = sum(scores[-100:]) / 100
            else:
                last_100_mean_score = sum(scores) / len(scores)
            last_100_mean_scores.append(last_100_mean_score)

            if agent.n_games % 200 == 0:
                plot(scores, mean_scores, last_10_mean_scores, last_100_mean_scores)

    last_200_scores = scores[-200:]
    last_200_moves = moves[-200:]
    statistics = compute_statistics(last_200_scores, last_200_moves)

    print_statistics(statistics)

if __name__ == '__main__':
    train()

Performance

Statistics for the last 200 games (PER agent):

Metric	Value
Average Score	32.12
Variance	172.31
Standard Deviation	13.13
Maximum Score	69
Minimum Score	8
Average Moves	455.50

The PER agent demonstrates improved performance compared to the standard DQN agent. The average score and maximum score are higher, indicating that the agent has learned more effective strategies for achieving higher scores. The reduced variance and standard deviation suggest that the PER agent’s performance is more consistent and stable.

Visualisation

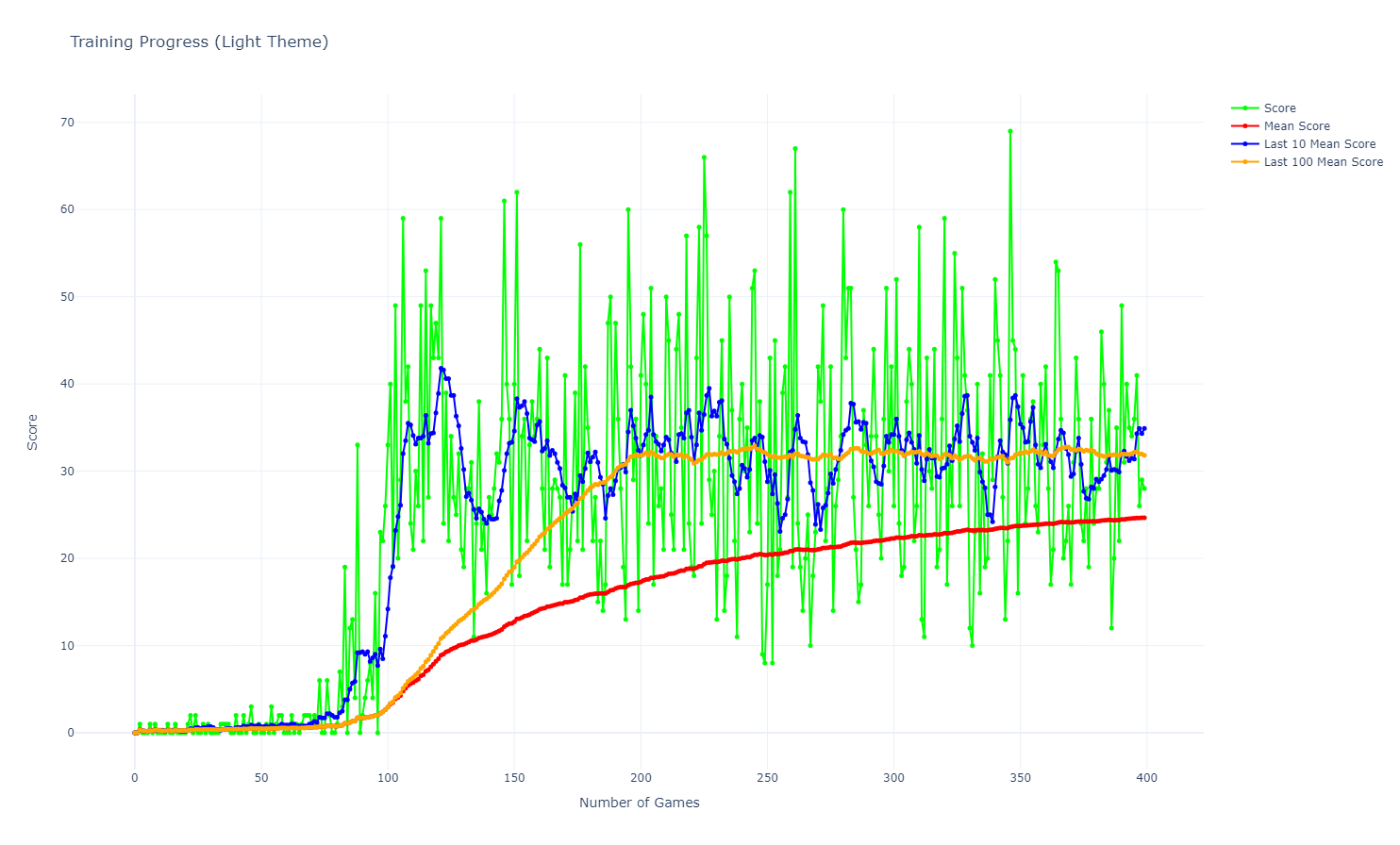
The graph shows the evolution of the average score, last 10 games average score, and last 100 games average score over the training episodes. The PER agent’s performance improves more rapidly and stabilizes earlier compared to the standard Q-learning agent. In the last 200 games, scores bellow 10 are rare, they only happen in 3 games, while the Q-learning agent had 10 games with scores bellow 10. The minimum score of 8 is a good indicator of the PER agent’s ability to avoid catastrophic failures.

Results Comparison

Method	Average Score	Variance	Std Deviation	Max Score	Min Score	Average Moves
Heuristic	15.48	67.26	8.20	41	1	295.60
Q-learning	30.64	170.99	13.08	66	1	788.80
DQN	29.16	152.71	12.36	65	1	1056.50
PER	32.12	172.31	13.13	69	8	455.50

The comparative analysis of the AI methods for the Snake game reveals the following insights:

• Heuristic Method: The heuristic method provides a simple baseline for the Snake game, achieving an average score of 15.48. However, the heuristic method has limited adaptability and learning capabilities, leading to suboptimal performance in complex scenarios.
• Q-learning: The Q-learning agent demonstrates significant improvements over the heuristic method, achieving an average score of 30.64. Q-learning learns optimal policies through exploration and exploitation, leading to better performance and higher scores than the heuristic method.
• DQN: The DQN agent builds on Q-learning by leveraging deep neural networks to approximate the Q-values. The DQN agent achieves an average score of 29.16, demonstrating the effectiveness of deep learning in reinforcement learning tasks. DQN agent has higher average moves per game compared to Q-learning, but the variance is lower.
• PER: The PER agent further enhances the DQN algorithm by prioritizing experiences based on their importance. The PER agent achieves the highest average score of 32.12, indicating improved learning efficiency and performance. The PER agent also demonstrates better results in terms of Average Score, Average Moves, Maximum Score, and Minimum Score compared to the other methods. The variance and standard deviation are slightly higher than Q-learning, but the model is less likely to have catastrophic failures.

Conclusion

The comparative analysis demonstrates the strengths and weaknesses of each AI method. While heuristic methods provide a simple baseline, reinforcement learning methods like Q-learning, DQN, and PER show significant improvements in performance, with PER achieving the highest performance.

References

1. Q-learning - Wikipedia ↩︎

2. Reinforcement Learning (DQN) - PyTorch ↩︎

3. Prioritized Experience Replay - Schaul et al ↩︎